Algoritmos #05 - Algoritmos de ordenação, parte II
Parte I: Algoritmos simples de ordenação
Continuando a série de posts sobre algoritmos de ordenação, trataremos agora dos algoritmos que utilizam os chamados métodos eficientes de ordenação, que, apesar de retornarem os resultados de forma mais ágil, apresentam mais difícil implementação, sendo, portanto, indicados para a resolução de problemas mais complexos.
Continuando a série de posts sobre algoritmos de ordenação, trataremos agora dos algoritmos que utilizam os chamados métodos eficientes de ordenação, que, apesar de retornarem os resultados de forma mais ágil, apresentam mais difícil implementação, sendo, portanto, indicados para a resolução de problemas mais complexos.
Métodos eficientes
Os dois métodos apresentados a seguir, Merge sort e Quick sort, utilizam, de formas diferentes, um paradigma bastante famoso na criação de algoritmos, através do qual eles conseguem uma performance mais eficiente: o ''dividir-para-conquistar''. Tal paradigma consiste na divisão do problema em várias partes menores, ou sub-problemas, que são similares ao problema original. Os sub-problemas são resolvidos de forma recursiva e depois são combinados em uma solução para o problema original.
- Merge Sort
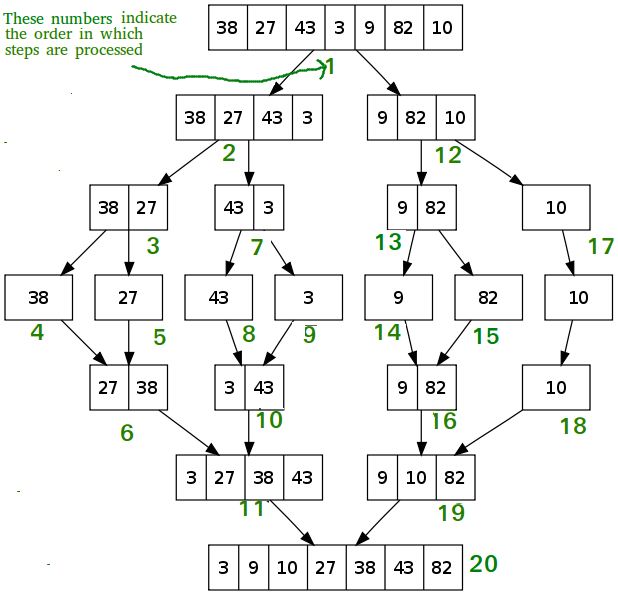
O Merge sort funciona da seguinte forma: a lista a ser ordenada é dividida em duas sub-listas de igual tamanho (divisão), que continuam a ser divididas em listas cada vez menores até que restem apenas dois elementos, já que a ordenação entre eles é bem simples (conquista utilizando-se da recursão). Na concatenação, os dois menores elementos de cada parte são separados e o menor entre eles é selecionado e retirado de sua parte. Em seguida, os menores entre os restantes são comparados e assim se prossegue até que o resultado seja uma versão ordenada da lista original.
O principal defeito do Merge sort é o gasto de memória, pois, para que a operação seja realizada, é criado um novo vetor, que é uma cópia do original. Por isso, ele é indicado apenas em casos de complexidade elevada, nos quais é necessário que a velocidade se mantenha constante, independentemente do caso.
O principal defeito do Merge sort é o gasto de memória, pois, para que a operação seja realizada, é criado um novo vetor, que é uma cópia do original. Por isso, ele é indicado apenas em casos de complexidade elevada, nos quais é necessário que a velocidade se mantenha constante, independentemente do caso.
- Quick Sort

Já no Quick sort, escolhe-se um número qualquer (chamado de pivô) e, a partir dele, ocorre o particionamento, no qual os números são divididos da seguinte forma: à esquerda do pivô, estão os números que são menores que ele e, à sua direita, os que estão os maiores. As sub-listas continuam a ser particionadas até que reste apenas uma lista unitária. Após isso, basta combinar as sub-listas já ordenadas e o resultado final é obtido.
Vale ressaltar que a escolha de qual número será o pivô pode afetar o desempenho do algoritmo, por isso, existem formas de escolhê-lo. Normalmente é selecionado o elemento central do vetor.
O Quick sort difere-se do Merge sort a medida que:
Vale ressaltar que a escolha de qual número será o pivô pode afetar o desempenho do algoritmo, por isso, existem formas de escolhê-lo. Normalmente é selecionado o elemento central do vetor.
O Quick sort difere-se do Merge sort a medida que:
- No Quick sort: a maior parte do trabalho é feita na etapa de divisão, as operações são feitas localmente (dentro do vetor original) e o desempenho é instável, pois, nos piores casos, assemelha-se ao de algoritmos simples.
- No Merge sort: a maior parte do trabalho é feita na etapa de combinação, as operações são feitas externamente (é criado um novo vetor) e o desempenho mantém-se estável na maioria dos casos.
Comparação
Na imagem acima, é possível analisar a velocidade de execução, em certas situações, de vários algoritmos de ordenação, incluindo os já apresentados no blog (Bubble sort, Selection sort, Insertion sort, Quick sort e Merge Sort) e alguns outros menos conhecidos. Perceba que é notória a disparidade entre os algoritmos simples e os eficientes, principalmente nos casos em que os vetores estão mais desorganizados.
É possível notar também as semelhanças e diferenças entre os métodos de uma mesma categoria. O Quick sort e o Merge Sort, por exemplo, concluem a execução com velocidade bem parecida nos casos mais simples. Entretanto, nos casos mais difíceis, o Merge sort se mostra um pouco mais rápido.
Tal análise mostra que algoritmos que realizam uma função idêntica podem apresentar várias peculiaridades, o que os tornam adequados para situações e necessidades diferentes. Por isso, é essencial refletir bastante antes de escolher qual algoritmo implementar em cada projeto.
Referências
https://www.treinaweb.com.br/blog/conheca-os-principais-algoritmos-de-ordenacao/
https://pt.khanacademy.org/computing/computer-science/algorithms/merge-sort/a/divide-and-conquer-algorithms
https://www.geeksforgeeks.org/merge-sort/
https://pt.khanacademy.org/computing/computer-science/algorithms/quick-sort/a/overview-of-quicksort
https://pt.khanacademy.org/computing/computer-science/algorithms/merge-sort/a/divide-and-conquer-algorithms
https://www.geeksforgeeks.org/merge-sort/
https://pt.khanacademy.org/computing/computer-science/algorithms/quick-sort/a/overview-of-quicksort

É legal estudar a análise de complexidade dos algoritmos. E, um dos mais frequentes na computação, são os algoritmos de ordenação. Em relação aos que foram mencionados, nunca ouvi falar do Shell e do Quick3. Aparentemente o Quick3 e o Quick são parecidos, mas o Quick é mais lento para "Few Unique" sabe comentar alguma diferença entre esses dois?
ResponderExcluirNo QuickSort comum existe a divisão do array em duas partes, de acordo com o pivô (maiores que o pivô e menores que o pivô), certo? O problema é que, quando existem elementos repetidos, eles têm que ser alocados em um dos dois lados, tendo que passar também pelo processo de ordenação, mesmo você já sabendo onde eles irão ficar (são iguais ao pivô, afinal).
ExcluirO QuickSort3 (3-way QuickSort) é basicamente um aprimoramento do QuickSort comum, em que o array é dividido em 3 partes (menores que o pivô, iguais ao pivô e maiores que o pivô). Por isso, ele é melhor em casos com muitos elementos repetidos, como no Few Unique da imagem.
Esse site tem uma explicação melhor, com exemplos: https://www.geeksforgeeks.org/3-way-quicksort-dutch-national-flag/
Então... No QuickSort3, o pivô é escolhido aleatoriamente ou há uma busca? Acho que entendi. É como se pegasse um vetor V e dividissse em três vetores V1, V2 e V3 em que no V1: os elementos menores do que o pivô, no V2: elementos repetidos que são iguais ao pivô, no V3: os elementos maiores que o pivô. E, depois retorna o vetor V ordenado.
ExcluirComo esta desigualdade: V1 <= V2 <= V3, em que quando há elementos iguais em mesma lista estão em ordem.
Ex.: [1, 2 ,2 , 2, 3, 4] (Depois de ter efetuado o QuickSort3)
A escolha do pivô depende mais do programador, tanto no QuickSort comum quanto no 3-way.
ExcluirE sim, o funcionamento é do jeito que você entendeu mesmo.
Este comentário foi removido pelo autor.
ResponderExcluir